A(M)Cademy of VIBROdiagnostics

27.09.2021

Uszkodzenia łożysk tocznych są jedną z najważniejszych przyczyn awarii maszyn wirnikowych. Wczesne wykrycie uszkodzenia łożyska pozwala na względnie tanią jego wymianę. Jeśli łożysko ulegnie degradacji, pojawiają się negatywne konsekwencje, produkty zużycia dostają się do oleju, praca wału ulega zmianie, co w konsekwencji zaczyna niszczyć kolejne elementy maszyny, np. przekładnie zębate, sprzęgła oraz inne łożyska. W skrajnych przypadkach, całkowite zniszczenia łożysk prowadzą do różnego rodzaju katastrof, np. katastrof lotniczych ^[1].

Analiza obwiedni sygnału

We wczesnej fazie rozwoju uszkodzenia, łożysko toczne wzbudza swoją strukturę i obudowę zgodnie z tzw. „charakterystyczną częstotliwością uszkodzenia”. Na razie przyjmijmy, że jest to jakaś częstotliwość, np. 90 Hz. Można sobie wyobrazić, że jest to taka sytuacja, kiedy maszyna nie pracuje, a jakiś mały młotek uderza w obudowę 90 razy na sekundę. Dalej, robimy pomiar, który trwa 1 sekundę. Jak będzie wyglądał taki sygnał? – Zobaczymy tzw. gasnące odpowiedzi impulsowe, jak pokazano na Rys. 1.

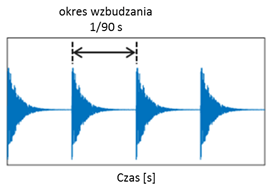
Rysunek 1 Gasnące odpowiedzi impulsowe

Rozwój nauki (analiza Fourierowska oraz analiza modalna) spowodował, że potrafimy kolejno odczytać i zinterpretować skład częstotliwościowy takiego sygnału, i to zarówno pojedynczej odpowiedzi impulsowej, jak i wielu odpowiedzi na raz. I tak, w przypadku typowych obudów łożysk, skład częstotliwościowy takiego sygnału wygląda jak różnego rodzaju „wzgórza” w paśmie od około 2kHz do około 10kHz, co schematycznie pokazano na Rys. 2.

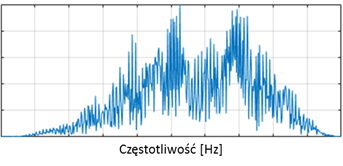
Rysunek 2 Widmo serii odpowiedzi impulsowych

Wyobraźmy sobie teraz, że mamy maszynę z uszkodzonym łożyskiem, która generuje odpowiedzi impulsowe, ale tym razem maszyna pracuje. Ponieważ pracuje, to generuje jeszcze inne bardzo liczne komponenty, ale z reguły te komponenty są w znacznie niższym paśmie częstotliwościowym, tj. typowo od kilku Hertzów do 2 kHz. Są to przede wszystkim częstotliwości pochodzące od wałów i przekładni, o których mówiliśmy w poprzednich postach. Co ważne, mają one dużo większą energię niż poszukiwane przez nas impulsy od łożysk.

Analiza obwiedniowa polega na usunięciu (odfiltrowaniu) komponentów sygnału w paśmie względnie niskim (wynik takiej operacji w dziedzinie częstotliwości przedstawia Rys. 2) oraz na znalezieniu odpowiedzi na pytanie jaki jest okres wzbudzania struktury (parametr zaznaczony na Rys. 1). Gdyby wszystkie sygnały drgań były łatwe w analizie, taką informację można by było zwyczajnie odczytać z przebiegu czasowego, tak, jak syntetycznym Rys. 1. Ale niestety z reguły, łożyska we wczesnej fazie rozwoju uszkodzenia generują sygnały, które są o całe rzędy wielkości niższe od innych komponentów sygnału, dlatego też odpowiedzi impulsowe nie są widoczne na przebiegach czasowych. Rys. 3 ilustruje takie porównanie.

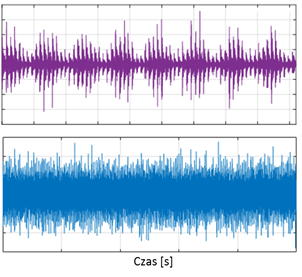
Rysunek 3 Góra: dobrze widoczne uszkodzenie, dół: słabo widoczne uszkodzenie

Jednym z najpowszechniejszych i najbardziej skutecznych sposobów na znalezienie cyklu wzbudzania struktury, czyli kolejnym etapem analizy obwiedniowej, jest konstrukcja całkowicie nowego sygnału, którego okres wyraża częstotliwość pojawiania się pulsów, jak pokazano na Rys. 4.

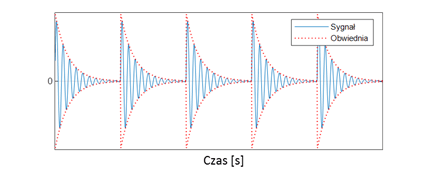
Rysunek 4 Nowy sygnał

Taki nowy sygnał konstruuje się poprzez filtrację sygnału czasowego zawierające drgania strukturalne przez filtr dolnoprzepustowy. Wcześniej (powód matematyczny, który pominiemy), sygnał odpowiedzi o wartościach ujemnych przekształcamy na wartości dodatnie (obliczamy tzw. „wartość bezwzględną”), czyli (mówiąc językiem elektroników) wykonujemy wyprostowanie sygnału. Niestety, dla danych, o których nic nie wiemy, dobór częstotliwości zaporowej filtru dolnoprzepustowego nie jest oczywisty, dlatego na przestrzeni lat powstało bardzo wiele technik alternatywnych. Sposób

filtr górnoprzepustowy -> wartość bezwzględna -> filtr dolnoprzepustowy

nie jest najefektywniejszy, ale bardzo pomaga pokazać istotę metody obwiedni. Dla ilustracji problemu, Rys. 5 przedstawia nasz „nowy sygnał” uzyskany przez filtrację dolnoprzepustową odpowiedzi impulsowych z różnymi wartościami częstotliwości zaporowej.

Rysunek 5 Dobór parametrów filtru LP w procesie generowania sygnału obwiedni

W dalszej części analizy, nasz „nowy sygnał” jest poddawany standardowej procedurze obliczenia widma, które nazywa się „widmem obwiedni”. Przykładowe widmo obwiedni pokazano na Rys. 6

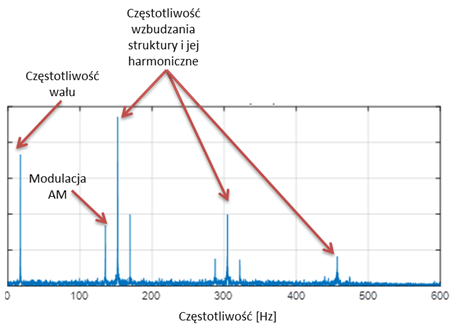
Rysunek 6 Przykładowe widmo obwiedni

Patrząc na Rys. 6, można powiedzieć, że istotną analizy obwiedniowej jest to, że nie szukamy częstotliwości strukturalnych, które są wzbudzane, ale szukamy częstotliwości, z jaką one są wzbudzane. Odwołując się do Rys. 1, częstotliwość wzbudzania drgań strukturalnych, która jest jedną z tzw. częstotliwości „charakterystycznych” łożyska jest równa odwrotności okresu ich wzbudzania.

Jak znaleźć częstotliwości charakterystyczne mojego łożyska?

Po wstępie, gdzie pokazaliśmy metody analizy obwiedni sygnału, wróćmy na chwilę do zdania z początku postu: We wczesnej fazie rozwoju uszkodzenia, łożysko toczne wzbudza swoją strukturę i obudowę zgodnie z tzw. „charakterystyczną częstotliwością uszkodzenia”. Spójrzmy na schemat łożyska tocznego (Rys.7).

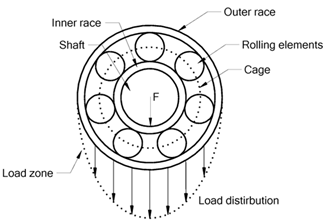
Rysunek 7 Budowa łożyska tocznego (kulkowego) ^[2]

Wzbudzenia impulsów pojawiają się, gdy pojawi się uszkodzenie na którymś ze współpracujących elementów. Jeżeli jest to np. bieżnia zewnętrzna (ang. Outer Race), wtedy przetoczenie się każdego elementu spowoduje mikrouderzenie i pojawienie się impulsu. Impuls wzbudzi strukturę obudowy łożyska, po czym wygaśnie. Za chwilę przetoczy się kolejny element toczny i sytuacja się powtórzy. Typowo, łożysko toczne (bo tylko o takich teraz mówimy) może  generować kilka częstotliwości charakterystycznych, które są zamieszczone w Tabeli 1.

Tabela 1 Częstotliwości charakterystyczne łożyska tocznego

Akronim	Rodzaj uszkodzenia	Wzór (uproszczony, 1 bieżnia nieruchoma)
BPFO (Ball Passing Frequency of the Outer Race)	Lokalne uszkodzenie bieżni zewnętrznej	(nf_r)/2 (1-d/D cosθ)
BPFI (Ball Passing Frequency of the Inner Race)	Lokalne uszkodzenie bieżni wewnętrznej	(nf_r)/2 (1+d/D cosθ)
BSF (Ball Spin Frequency)	Uszkodzenie elementu tocznego (uderzenie o jedną bieżnię)	f_r D/2d [1-(d/D cosθ)^2 ]
FTF (Fundamental Train Frequency) albo Cage	Uszkodzenie koszyka	f_r/2 (1-d/D cosθ)

gdzie:

• d – średnica elementu tocznego
• D – średnica podziałowa łożyska (odległość między środkami przeciwległych el. tocznych)
• n – ilość elementów tocznych (w jednym rzędzie)
• fr – prędkość wału- kąt obciążenia (typowo zero stopni)

Częstotliwości charakterystyczne można łatwo uzyskać w programie VIBnavigator w zakładce „Kinematics Editor”, wprowadzając ww. dane, co pokazano na Rys. 7. Częstotliwości te są również dostępne na stronach internetowych producentów łożysk.

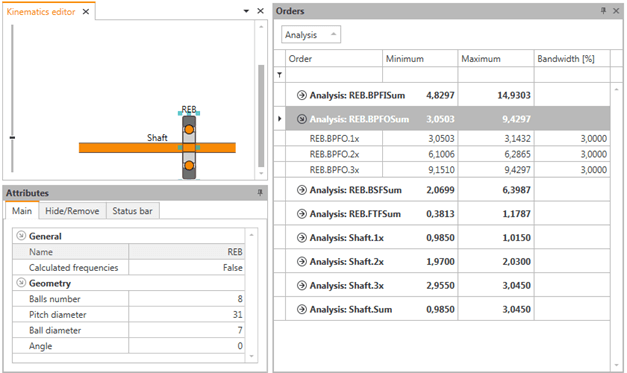
Rysunek 8 Automatyczne obliczanie częstotliwości charakterystycznych łożyska

Z Rys. 8 można odczytać, że przykładowo fundamentalna częstotliwość BPFO będzie śledzona w paśmie 3,05Hz-3,14 Hz.

Przykład rzeczywisty

Na rys. 9 pokazano sygnał rzeczywistego dla łożyska w poprawnym stanie technicznym oraz łożyska z uszkodzoną bieżnią wewnętrzną. Wykresy wykonano w środowisku VIBnavigator, a dane zebrano systemem AVM 4000.

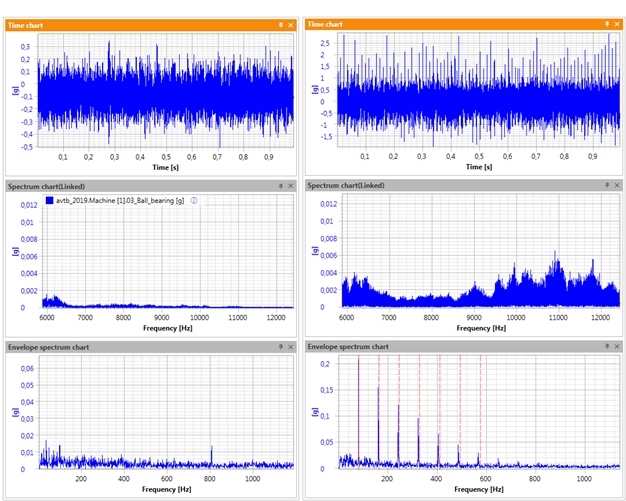
Rysunek 9 Porównanie łożysk: lewa – łożysko dobre, prawa – łożysko uszkodzone

Wykresy górne na Rys. 9 pokazują przebiegi czasowe. Należy zwrócić uwagę nie tylko na charakterystyczne „szpilki” na wykresie, ale również na poziom wartości na osi poziomej – dla przykładowego, znacznego uszkodzenia, wzrost wartości jest znaczny. Na wykresach środkowych widzimy, że uszkodzone łożysko wzbudza drgania strukturalne w zakresie 6kHz-12kHz. Wreszcie, na widmie obwiedni (wykresy dolne), dla poprawnego łożyska widzimy praktycznie szum pomiarowy, a dla uszkodzonego widzimy kolejne harmoniczne częstotliwości BPFO. Z reguły, systemy monitorowania ciągłego przeprowadzają detekcję uszkodzeń łożysk poprzez pomiar wartości PP oraz wartości RMS (zob. Post nr 2) sygnału obwiedni, a dalej identyfikację rodzaju uszkodzenia poprzez śledzenie indywidualnych częstotliwości charakterystycznych, np. sumy komponentów BPFOx1, BPFOx2 i BPFOx3. Materiałów z zakresu diagnostyki łożysk jest wiele. Szczególnie polecamy tzw. Primers and handbooks ze strony ^[3], na początek szczególnie pozycje Primer 1982 i Primer 1983 oraz książkę ^[4].

Zastosowanie aparatury pomiarowej

Firma AMC VIBRO oferuje systemy, które pozwalają zarówno na detekcję, jak i identyfikację i ocenę poziomu uszkodzenia łożysk tocznych zdefiniowanych automatycznie na podstawie modelu kinetostatycznego. Użytkownik w prosty sposób metodą „drag and drop” tworzy układ kinematyczny swojej maszyny, a program VIBnavigator wylicza wszystkie częstotliwości charakterystyczne.

	AVM 1000	AVM 2000	AVM 4000
Detekcja poważnego uszkodzenia łożyska analizą VRMS	✔️	✔️	✔️
Detekcja wczesnego rozwoju uszkodzenia poprzez śledzenie pasm widma		✔️	✔️
Detekcja wczesnego rozwoju uszkodzenia poprzez śledzenie komponentów widma obwiedni		✔️	✔️
Automatyczna identyfikacja rodzaju uszkodzenia			✔️
Analiza widma obwiedni			✔️
Automatyczna konfiguracja częstotliwości charakterystycznych łożyska			✔️

Referencje

^[1] https://doi.org/10.1016/S1350-6307(98)00024-7

^[2] Barszcz, Vibration-Based Condition Monitoring of Wind Turbines, Springer 2019

^[3] https://www.bksv.com/en/knowledge/library/technical-reviews

^[4] R.B. Randall, Vibration‑based Condition Monitoring, John Wiley & Sons, Ltd, 2010

Polecamy