A(M)Cademy of VIBROdiagnostics
#6_2 Diagnostyka drganiowa przekładni - dla dociekliwych
W poprzednim poście
W pierwszej części posta o diagnostyce przekładni podaliśmy trochę podstawowych informacji z różnych perspektyw, aby pokazać, jak obszerny jest to temat. Wyjaśniliśmy pojęcie częstotliwości charakterystycznych przekładni i pokazaliśmy, jak konstruowana jest częstotliwość GMF dla prostego układu maszynowego. Następnie zilustrowaliśmy, jak obliczone częstotliwości przekształcane są (wewnątrz systemu CMS) na pasma widmowe, z których obliczane są trendy – czyli źródła danych wejściowych do generowania alarmów. W dalszej części postu, podaliśmy ogólna klasyfikację uszkodzeń przekładni i przedstawiliśmy podstawowe techniki analizy wibrodiagnostycznej.
W niniejszym poście, kierowanym do czytelników dociekliwych, przedstawimy szerzej wybrane zagadnienia diagnostyki przekładni, które w zamyśle pomogą rozwiązać trudności pojawiające się np. w analizie skomplikowanych maszyn.
Wybrana terminologia
Im bardziej się zagłębimy w budowę przekładni, tym bardziej potrzebna jest specjalistyczna wiedza – związana np. z obliczeniami naprężeń zginających i ściskających czy obliczaniem wskaźników przyporu (bardzo ciekawy dział konstrukcji maszyn). W naszym słowniczku ograniczymy się jednak do kilku najważniejszych pojęć, które często pojawiają się w kontekście analizy diagnostycznej, choćby po to, aby poprawnie opisać miejsce uszkodzenia i skonsultować sposób naprawy.
- Budowa koła zębatego
W celu opisu budowy koła zębatego, posłużymy się popularnym w literaturze Rys. 1
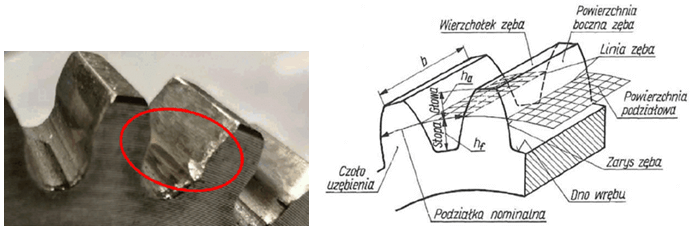
Rys. 1 Zdjęcie fragmentu koła zębatego i jego parametry [1]
Przykładowo, korzystając z terminologii na Rys. 1, możemy precyzyjnie opisać w rozmowie, że pitting na zdjęciu z lewej strony występuje na krawędzi czoła uzębienia oraz powierzchni bocznej zęba.
- Moduł zęba
Jest to parametr każdego koła zębatego, który musi być identyczny, aby koła mogły ze sobą poprawnie współpracować. Ze względu na obowiązujące normy, moduł określa zarówno wymiary zębów, jak i kół zębatych. Dokładne obliczenia są ogólnie dostępne – my zwrócimy uwagę na to, że „Podziałka nominalna p” zaznaczona na Rys. 1 jest również nazywana „Podziałką” lub „Podziałką obwodową„. Bezpośrednio z tym elementem związane są fundamentalne pojęcia okręgu podziałowego (zwanego też kołem podziałowym – okręgu złożonego z kolejnych podziałek p) oraz średnicy podziałowej – d, czyli średnicy koła zębatego łączącej dwa przeciwległe punkty podziałki nominalnej. Przy użyciu tych pojęć konstruuje się dwa równoważne równania, które po przyrównaniu i podstawieniu liczby zębów – z, stanowią podstawę do wzorów dostępnych w literaturze:
obwód koła zębatego (po linii okręgu podziałowego)=2∙π∙r=π∙d
obwód koła zębatego (po linii okręgu podziałowego)=p∙z
π∙d=p∙z → p/π=moduł „m”=d/z
Znormalizowane wartości zawierające wartości modułów można znaleźć np. w normie PN/M-88502.
- Zębnik i koło zębate
Zębnik to koło o mniejszej średnicy w parze współpracujących kół zębatych (również koło zębate, które współpracuje z listwą zębatą). Koło o większej średnicy najczęściej nazywa się po prostu „kołem zębatym”. W jęz. angielskim , zębnik to pinion, który współpracuje z „gear” albo z „rack„. Podręczną i obszerną listę haseł w języku angielskim w tym temacie można znaleźć w [2].
Przekładnie obiegowe
Kiedy zabieramy się za diagnostykę techniczną przekładni obiegowej, najlepiej zacząć od dużej kawy, gdyż przekładnie obiegowe szybko stają się bardzo skomplikowanymi układami. Dzieje się tak dlatego, że posiadają one planety, które wprowadzają dodatkowy element ruchomy. Ten element nie tylko sam dodaje paczkę nowych częstotliwości charakterystycznych, ale również wpływa na wszystkie pozostałe częstotliwości charakterystyczne. Rys. 2 pokazuje jak zmienia się ruch punktu na planecie w zależności od tego, który element przekładni obiegowej jest nieruchomy.
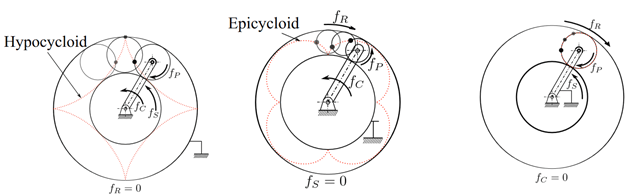
Rys. 2 Ścieżka wytyczona przez punkt na planecie dla różnych konfiguracji przekładni obiegowej, a) nieruchome koło główne – czyli przekładnia „planetarna”, b) nieruchome koło słoneczne, c) nieruchome jarzmo [3]
W konsekwencji, wystarczy wyobrazić sobie, że aby obliczyć częstotliwości charakterystyczne łożyska planety trzeba:
- uwzględnić ustawienie przekładni względem referencyjnego pomiaru prędkości,
- wiedzieć, który element jest nieruchomy,
- dodać albo odjąć prędkość obrotu planety względem siebie,
- dodać albo odjąć prędkość obrotu planety względem wału głównego.
Szczegółowy opis terminologii ruchu przekładni obiegowych wraz z bardzo cennymi rysunkami i wzorami czytelnik znajdzie w pozycji [3]. Pamiętajmy jednak, że kiedy natrafimy na zintegrowany, nietypowy układ wielostopniowy, to dopiero początek analizy. W terminologii dotyczącej przekładni obiegowych też szybko natrafimy na rozbieżności. Pierwsze rozbieżności dotyczą jej konfiguracji (z uwagi na to, że wariant z nieruchomym kołem główny jest najbardziej popularny, przekładnie obiegowe często nazywane są „planetarnymi”). Drugie rozbieżności dotyczą elementów przekładni („koło główne” albo „wieniec”). Trzecie rozbieżności, najtrudniejsze, dotyczą nieujednoliconych nazw częstotliwości charakterystycznych oraz prędkości względnych elementów przekładni obiegowych i ich łożysk (dlatego często mają w systemach CMS długie, opisowe nazwy).
Obliczenia dla trudnych przypadków
Tematyka wzorów dla skomplikowanych układów przekładni jest dość niewdzięczna, gdyż trudno znaleźć tutaj niekwestionowany autorytet – zarówno jeśli chodzi o zasadę obliczeń, jak również o nazwy częstotliwości charakterystycznych.
UWAGA! Na przestrzeni lat pojawiło się dużo publikacji oraz dedykowanych kalkulatorów zawierających błędy obliczeniowe oraz uproszczone założenia, stąd radzimy sprawdzać istotne obliczenia ze znanymi zasadami teoretycznymi.
W poprzednim poście podaliśmy ogólną zasadę obliczenia częstotliwości GMF (tj. V*Z), ale w przypadku wielostopniowych układów, szczególnie dla przekładni obiegowych, sformułowanie poprawnych równań jest dużo bardziej skomplikowane. Dodatkowo, wiele konstrukcji jest niestandardowych, a ponadto zęby kół zębatych mogą być modyfikowane (inaczej „korygowane„), co powoduje, że liniowa zależność pomiędzy średnicą kół i ich prędkością kątową nie jest zachowana. Oprócz [3], szczególnie cenna literatura w tym zakresie obejmuje ogólnie dostępne równania Willisa opracowane w 1891 r., pracę Fergussona z roku 1983 [4] oraz rozprawę doktorską Kurtha z roku 2012 [5]. Dodatkowo, w licznych pracach Erica Bechhofera oraz Waltera Bartelmusa można znaleźć analizę wielu konkretnych przypadków złożonych układów przekładni. Jednak na próżno jest szukać jednego narzędzia czy wzoru, który może być użyty w sposób zautomatyzowany do wszystkich istniejących konstrukcji przekładni. Tutaj część pracy pozostaje ręczna. W poście podamy podstawowe wzory dla najpopularniejszego wariantu przekładni obiegowych z nieruchomym kołem głównym, tj. dla przekładni planetarnej:
Znana prędkość koła głównego fR=0
Znana prędkość wejściowa koła słonecznego=fS
Prędkość wyjściowa jarzma fC= Zs/(Zs+Zr)*fS
Prędkość planety fP=(-Zs(Zr-Zp))/(Zp(Zs+Zr))*fS
GMF=(Zs*Zr)/(Zs+Zr)*|fS|=Zr*|fC|
gdzie:
fR, fS, fC – prędkość koła głównego, słonecznego i jarzma
Zr, Zs, Zp – ilość zębów na kole głównym, kole słonecznym i planecie
Lepiej zrozumieć sygnały drgań przekładni
W ramach omawiania interpretacji komponentów GMF oraz ich wstęg bocznych (SB), w części pierwszej postu o przekładniach wspomnieliśmy, że stosowanie tych samych reguł interpretacyjnych dla przekładni różnego rodzaju (szczególnie dla przekładni pracujących w różnych warunkach operacyjnych) nie jest podejściem prawidłowym. Dlaczego? Zacznijmy od prostego wyjaśnienia enigmatycznej „nieliniowości„.
Na ten moment uwierzmy na słowo, że każda maszyna z przekładnią to obiekt nieliniowy. Co to znaczy? Co do zasady, obiekt liniowy to taki, który nie zmienia częstotliwości sygnału wejściowego. Dla naszej przekładni jako modelu pewnego systemu, wzbudzeniem systemu jest częstotliwość wału wejściowego IN (z poprzedniego posta wartość 1) oraz wału wyjściowego OUT (z poprzedniego posta wartość 0.34), jak również częstotliwość zazębiania GMF (z poprzedniego posta wartość 23). Gdyby układ był liniowy, na widmie widzielibyśmy tylko te komponenty, tj. po kolei 0.34, 1 i 23, a nie częstotliwości GMF z grupą wstęg bocznych, jak pokazano na Rys. 4 w poprzednim poście (dla wygody czytelnika rysunek powtarzamy) jako Rys. 3.
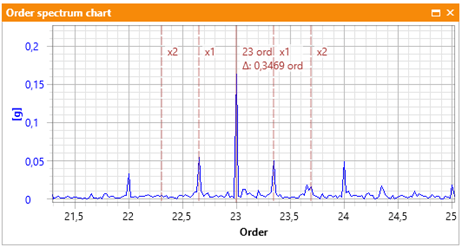
Rys. 3 Widmo w sąsiedztwie częstotliwości GMFx1 przekładni (zob. Rys. 4 z poprzedniego posta)
W przekładniach pojawiają się modulacje sygnałów drgań, a ich źródłem są właśnie nieliniowości układu. Modulacje są tematem odrębnym (teoria modulacji jest najobszerniej przedstawiana w telekomunikacji), ale w tym miejscu podamy najistotniejsze informacje w ujęciu praktycznym: przekładnie zębate generują wszystkie trzy rodzaje modulacji, tj. amplitudową (AM), częstotliwościową (FM) oraz fazową (PM), co wynika zarówno z tego, że każdy z wałów obraca się „nieidealnie” równo względem swojej teoretycznej osi obrotu oraz z tego, że podczas każdego kontaktu pary zębów następuje ich chwilowe ugięcie. Na potrzeby naszych rozważań nie będziemy rozróżniać poszczególnych modulacji, a zastanówmy się nad ich efektami w pracy przekładni. Tak więc, jakie to wszystko ma konsekwencje? – Przypomnijmy sobie na chwilę, że każde widmo z akcelerometru jest (w uproszczeniu, w dziedzinie częstotliwości) wynikiem pomnożenia widma sił działających na maszynę (wymuszeń) oraz charakterystyki maszyny (rozmiar, materiał i kształt), która nazywa się odpowiedzią częstotliwościową układu. Nieliniowość przekładni powoduje, że ten drugi składnik naszego sygnału z akcelerometru zmienia się wraz z parametrami pracy przekładni, ale przede wszystkim, że pojawiają się częstotliwości nieobecne w wymuszeniu. Dlatego przykładowo, przekładnia w bardzo dobrym stanie technicznym, jeśli będzie nieobciążona, może praktycznie nie generować wstęg bocznych, ale obciążona – może generować już bardzo silne wstęgi. I w tym miejscu podsumujmy ten temat – zamiast matematycznie skomplikowanej analizy zmiennej sztywności przekładni, w wyniku pewnego skrótu inżynierskiego, ogólnie przyjmuje się, że w ogóle nie powinno się wykonywać pomiarów diagnostycznych przekładni przy obciążeniu mniejszym od 40% jej obciążenia nominalnego.
UWAGA! Modulacyjny charakter sygnału drgań przekładni zębatych jest powodem opracowywania wielu zaawansowanych technik diagnostycznych opartych na (tzw. chwilowej) demodulacji częstotliwościowej i demodulacji fazowej. Dla dociekliwych polecamy publikacje P.D.McFaddena i R.B. Randalla w tej tematyce.
Drugim tematem, który jest niezbędny, aby zrozumieć problematykę analizy diagnostycznej przekładni jest wyjaśnienie jeszcze bardziej – przynajmniej na pierwszy rzut oka – enigmatycznej funkcji sztywności zazębiania (z ang. Meshing Stiffness Function – MSF). Wspomnieliśmy już o modulacjach spowodowanych uginaniem się zębów przekładni, które przekłada się bezpośrednio na obecność i wartość komponentów widma. Ale czy wszystkie zęby uginają się tak samo? Otóż, zdecydowanie tak nie jest. Wyobraźmy sobie, jak wygląda kontakt zębów śrubowych (lewa strona Rys. 4 – góra) w porównaniu z kontaktem zębów prostych (lewa strona Rys. 4 – dół). Schematyczny wynik takiej analizy sił przedstawiono na Rys. 4 po prawej stronie.
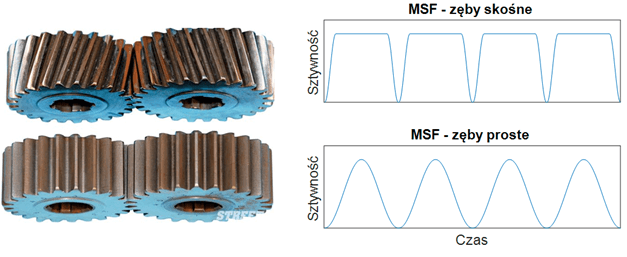
Rys. 4 Porównanie zazębiania dla zębów śrubowych (zwanych potocznie „skośnymi”, z ang. helical) i prostych (z ang. straight) [6] oraz ich schematycznych funkcji sztywności zazębiania (z ang. MSF – Meshing Stiffeness Function)
Praktyczna konsekwencja tego zjawiska oznacza, że oprócz parametrów operacyjnych, rozwiązania konstrukcyjne indywidualnych przekładni mają również bardzo duży wpływ na wzorzec widma przekładni dobrej i uszkodzonej. W literaturze najczęściej pojawia się analiza pierwszych trzech harmonicznych częstotliwości zazębiania (GMF) oraz ich pierwszych podwójnych wstęg bocznych. Typową wskazówką diagnostyczną jest na przykład stwierdzenie, że wzrost amplitudy wstęg bocznych ponad GMF (albo amplituda GMFx2 większa od GMFx1) są symptomami istotnych uszkodzeń przekładni. I owszem, tak się często zdarza, ale można również spróbować porównać prace Prof. Bartelmusa [7], w których analizowanych jest pierwszych 15 harmonicznych częstotliwości zazębiania z nowoczesnymi przekładniami obiegowymi dla turbin wiatrowych, które praktycznie nie generują częstotliwości GMF. Uwagi i odniesienia do głównych aspektów projektowania takich przekładni można znaleźć w [8]. Warto podkreślić, że przytoczone rozbieżności wynikają m.in. z tego, że różne konstrukcje przekładni charakteryzują się bardzo różną pracą zębów (czyli właśnie funkcją sztywności zazębiania), co powoduje, że podczas pracy w tych samych warunkach, ich zęby ulegają innym odkształceniom, generując inne wartości modulacji – i w ten sposób dochodzimy do ostatecznych różnych poziomów „prążków” GMF oraz „prążków” wstęg bocznych na widmie. Podsumowując, im funkcja MSF bardziej płaska (zob. prawa strona Rys. 4 – góra), tym praca przekładni jest ogólnie lepsza (uginanie się zębów jest mniejsze), a w konsekwencji komponent GMF ma mniejszą amplitudę.
Po trzecie, zauważmy, że przekładnie to systemy ograniczone obudową, która charakteryzuje się niezwykle skomplikowaną łączną funkcję przejścia od źródła defektu na kole zębatym do czujnika. Na Rys. 5 przedstawiono przykładowe ścieżki, jakimi może wędrować sygnał uszkodzenia dla różnych uszkodzeń elementów przekładni obiegowej w konfiguracji planetarnej.
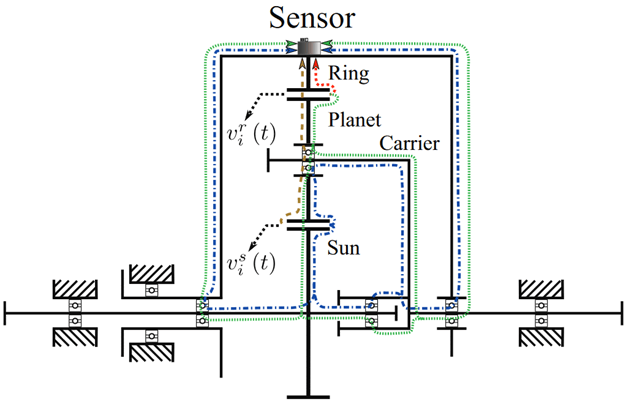
Rys. 5 Schemat funkcji przejścia sygnałów uszkodzeń [3]
Na Rys. 5 zaznaczono ścieżkę dla komponentu zazębiania pomiędzy planetą i kołem głównym oraz planetą i kołem słonecznym. Jak widać, w obu przypadkach, ten sam komponent wędruje różnymi ścieżkami do miejsca, w którym jest czujnik drgań i to w dodatku z różnych stron obudowy.
Praktyczna diagnostyka
Podsumowując informacje z obu postów o przekładniach – zwracamy uwagę czytelnika, że nie ma czegoś takiego, jak jeden wzorzec spektralny dla danej przekładni dobrej, a już w ogóle trudno wyobrazić sobie jeden wzorzec widmowy dla przekładni różnego rodzaju w poprawnym stanie technicznym. Pamiętajmy, że widmo sygnału przekładni jest wynikiem bardzo licznych czynników – nie tylko jej stanu technicznego, ale również cech konstrukcyjnych oraz parametrów operacyjnych. W konsekwencji, niestety dość łatwo jest uzyskać podobne widma dla dwóch różnych przekładni, z których jedna jest w dobrym stanie technicznym, a inna nie. Również bardzo łatwo jest uzyskać istotnie różne widma dla tej samej przekładni w danym stanie technicznym dla różnych parametrów jej pracy, czy różnych lokalizacjach czujnika. Co więcej, zależność obserwowanych komponentów widmowych od parametrów pracy, tj. głównie od prędkości obrotowej i obciążenia z reguły jest zupełnie inna dla różnych przekładni w zależności od ich konstrukcji oraz od ich rozmiaru (czyli mocy nominalnej). W konsekwencji, komponenty widmowe generowane przez niektóre przekładnie wykazują bardziej widoczną zależność od zmiany mocy, a inne od zmiany prędkości – a i takie stwierdzenie często jest prawdziwe tylko w pewnych przedziałach parametrów operacyjnych. No dobrze, ale jak sobie z tym wszystkim radzić? – Na koniec kilka praktycznych porad:
- ✔️ Rejestruj drgania na obudowie jak najbliżej węzłów łożyskowych
- ✔️ Rejestruj drgania zawsze w tym samym miejscu i kierunku
- ✔️ Porównuj sygnały (trendy) z tego samego czujnika przy niezmienionym mocowaniu
- ✔️ Zachowaj minimum 40% obciążenia nominalnego przekładni
- ✔️ Stosuj się do min. czasu pracy do osiągnięcia nominalnej temp. oleju (może być nawet 1h)
- ✔️ Rejestruj sygnały przy maksymalnie ograniczonej zmianie prędkości obrotowej (generalnie, im wyższa prędkość obrotowa, tym lepiej)
- ✔️ Zbadaj, ile GMF-ów może generować przekładnia (min. śledź 3, ale bywa aż do kilkunastu)
- ✔️ Dokonaj uproszczonej analizy modalnej (uderz w obudowę i zobacz, jak charakterystyka amplitudowo-częstotliwościowa) wpłynie ogólnie na śledzone komponenty widmowe
- ✔️ Dowiedz się, jakie zęby ma przekładnia, aby oszacować łatwość generowania GMF vs. SB
- ✔️ Upewnij się, że częstotliwości charakterystyczne zostały poprawnie obliczone
Stosuj technikę TSA, a przynajmniej widma uśrednione w analizie rzędów (typowo stosowane widma pełnej rozdzielczości mogą zmieniać poziomy komponentów nawet o połowę!)
Powodzenia!
- [1] Dobrzański T., Rysunek Techniczny Maszynowy, Wydawnictwo Naukowe PWN, Warszawa 2020
- [2] https://en.wikipedia.org/wiki/List_of_gear_nomenclature
- [3] C. M. Viduna, PhD Thesis, 2009 (https://theses.eurasip.org/media/theses/documents/molina-vicuna-cristian-contributions-to-the-analysis-of-vibrations-and-acoustic-emissions-for-the-condition-monitoring-of-epicyclic-gearboxes.pdf)
- [4] J. Ferguson, „Short cuts for analyzing planetary gearing”Mach. Des.,vol. 55, pp. 55-58, 1983
- [5] Franz Kurth, Efficiency Determination and Synthesis of Complex-Compound Planetary Gear Transmissions, Technischen Universität München, 2012
- [6] Michael Fernie, The Advantages And Disadvantages Of Straight Cut Gears, 2016 (https://www.carthrottle.com/post/the-advantages-and-disadvantages-of-straight-cut-gears/)
- [7] Bartelmus, R. Zimroz, A new feature for monitoring the condition of gearboxes in non-stationary operating conditions, MSSP, 2009 https://www.sciencedirect.com/science/article/abs/pii/S0888327009000132
- [8] C. Halse, Wind Turbine Drivetrain Development, 2012 https://www.nrel.gov/wind/assets/pdfs/05_1_halse_wind_turbine_drivetrain_development.pdf