A(M)Cademy of VIBROdiagnostics

24.06.2021

Rozosiowanie, obok niewyrównoważenia, jest jednym z najczęstszych stanów uszkodzenia w typowych maszynach wirnikowych. Jak sama nazwa wskazuje, rozosiowanie (zwane bardziej formalnie „niewspółosiowością”) ma miejsce wtedy, gdy dwa obracające się wały (połączone sprzęgłem) nie leżą w jednej osi. Ponieważ rozosiowanie z reguły generuje tzw. „komponenty harmoniczne”, pojęcie to też zostanie wyjaśnione w dalszej części posta.

Rodzaje rozosiowania

Podobnie, jak w przypadku niewyrównoważenia, trzeba zaznaczyć, że problem „rozosiowania” może być rozpatrywany z dwóch głównych perspektyw:

• w przypadku analizy pracy wałów maszyn dużej mocy (z reguły są to maszyny energetyczne), rozosiowanie linii wałów jest skomplikowanym zjawiskiem dynamicznym, które jest związane m.in. z przemieszczeniem podpór łożyskowych oraz tzw. nierównoległości osi panwi w stosunku do osi czopów łożyskowych. W analizie takiej stosuje się pomiary drgań względnych, na podstawie których wykreśla się różnego rodzaju obrazy drgań węzłów łożyskowych, drgań własnych, trajektorii wałów, itd.
• w przypadku analizy pracy układów napędowych największej grupy maszyn wirnikowych pracujących w przemyśle (objętych normą ISO 20816), którymi będziemy się zajmować w tym poście, rozosiowanie dotyczy sytuacji, w której dwa wały połączone sprzęgłem nie pracują w jednej osi. W maszynach tego rodzaju, wyróżniamy dwa główne rodzaje rozosiowania: rozosiowanie równoległe – kiedy osie pracy wałów są różne, ale równoległe oraz rozosiowanie kątowe – kiedy osie wałów są pod kątem względem siebie, co pokazano na Rys. 1. Dodatkowo, w przypadku gdy rozosiowanie kątowe ma miejsce w różnych płaszczyznach, można mówić podkreślić ten fakt nazywając rozosiowanie „przestrzennym”.

Rysunek 1 Rodzaje rozosiowania typowych maszyn wirnikowych

Terminologia

Typowo literatura podaje, że rozosiowanie generuje tzw. komponent „2x”. Jest to stwierdzenie ogólnie słuszne, ale nie zawsze. Zanim uzasadnimy źródło wątpliwości, zacznijmy od wyjaśnienia, co ten skrót oznacza. Symbol „2x” odnosi się do częstotliwości dwukrotnie większej, niż częstotliwość referencyjna. W diagnostyce maszyn, częstotliwość referencyjna to (prawie zawsze) częstotliwość wału napędowego, którą oznaczamy „Shaft 1x” albo w skrócie „1x”. W takim razie, 1x jest to również prędkość obrotowa maszyny (wyrażona w Hz, a po przemnożeniu przez 60 – wyrażona w RPM). Warto zwrócić uwagę, że część osób nazwa 1x częstotliwością fundamentalną, a część osób „pierwszą harmoniczną”, dlatego też opisywany komponent „2x” nazywany jest często „drugą harmoniczną”, w domyśle „wału napędowego”.

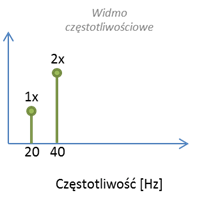
Rysunek 2 Komponent „1x” i komponent „2x” w dziedzinie częstotliwości

Na Rys. 2 schematycznie przedstawiono widmo częstotliwościowe z komponentem 1x, odpowiadające prędkości obrotowej maszyny równej 20 Hz oraz z komponentem 2x odpowiadającym częstotliwości 2*20 Hz = 40 Hz (40 * 60 RPM = 2400 RPM).

Kilka słów więcej o harmonicznych

Chwilowo, zabierzemy czytelnika do świata teorii przetwarzania sygnałów (bez obaw, wzorów nie będzie). Przypomnijmy tylko trzy fakty:

1. Zgodnie z analizą Fourierowską, każdy sygnał rzeczywisty można reprezentować za pomocą zbioru komponentów sinusoidalnych (innymi słowy: z każdego sygnału drgań można policzyć widmo),
2. Pojedynczy komponent sinusoidalny w dziedzinie czasu jest reprezentowany jako pojedynczy komponent (tzw. „prążek” widmowy) w dziedzinie częstotliwości,
3. Wg. teorii, „idealny” puls w dziedzinie czasu (tj. taki, który jest nieskończenie wąski i który „od razu” osiąga nieskończoność – tzw. „delta Diraca”) jest reprezentowany jako linia horyzontalna w dziedzinie częstotliwości.Nawet bez precyzyjnego aparatu matematycznego, na podstawie przytoczonych faktów, dokonując wizualnej analizy „wstecz”,  można dojść do wniosku, że sygnał, którego widmo składa się z dwóch albo więcej komponentów sinusoidalnych w dziedzinie czasu, jest wyrażony w (oryginalnej) dziedzinie czasu za pomocą odpowiedniej ilości komponentów sinusoidalnych, co pokazano schematycznie na Rys. 3.

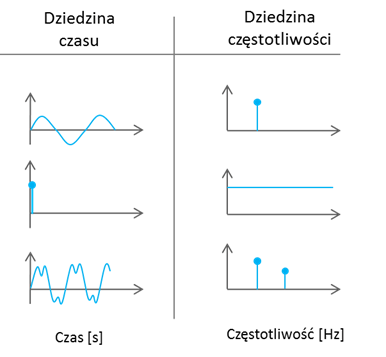
Rysunek 3 Ideowe reprezentacje sygnałów w dziedzinie czasu i częstotliwości, od góry: komponent sinusoidalny, puls oraz dwa komponenty sinusoidalne

W praktycznej analizie sygnałów, z rys. 3 płyną dwa główne wnioski:

1. Im badany sygnał jest bliżej idealnego sinusa, tym jego reprezentacja widmowa jest bliższa pojedynczemu komponentowi (tj. „prążkowi”),
2. Jeśli sygnał czasowy jest „daleki” od idealnego sinusa w sposób powtarzający się, to na widmie będą widoczne prążki w równych odstępach od siebie – czyli tzw. harmoniczne.

Z uwagi na to, że w analizie diagnostycznej sygnałów drgań komponenty harmoniczne  są związane z nieidealnym ruchem sinusoidalnym, ich obecność (szczególnie wzrost) jest bardzo istotnym symptomem rozwoju uszkodzenia.

Teraz wróćmy do konkretnego tematu rozosiowania.

Wykrywanie rozosiowania

Jak wspomnieliśmy, typowo podaje się, że rozosiowanie jest wykrywane poprzez śledzenie drugiej harmonicznej wału 2x – dlaczego? Pomoże tutaj przykład rowerzysty, który jedzie przed nami i który ma krzywe koło, jak na Rys. 4.

Rysunek 4 Analogia rozosiowania maszyny wirnikowej

W prostym przypadku, łatwo zauważymy, że koło roweru wykonuje dwa ruchy w płaszczyźnie przed nami, dlatego że w pierwszym ruchu „ucieka” od swojego miejsca, a w drugim „wraca” na swoje miejsce – a przecież sytuacja musi się powtarzać raz na obrót. Stąd, częstotliwość „drgań” jest dwukrotnie większa niż częstotliwość obrotu. W przypadku wałów maszyn wirnikowych, sytuacja jest analogiczna – każdy ruch wałów, który odbiera od teoretycznej wspólnej osi, musi zostać skompensowany w trakcie każdego kolejnego obrotu.

Jednakże w praktyce, manifestacja rozosiowania wałów maszyn wirnikowych nie zależy tylko od rodzaju rozosiowania (zob. Rys. 1), ale również od sposobu, w jaki sposób wały są ze sobą połączone, czyli konkretnie od rodzaju sprzęgła. Główne rodzaje sprzęgieł spotykane w maszynach wirnikowych obejmują sprzęgła sztywne, podatne lub zębate. Przykładowo, sprzęgła podatne dopuszczają pewien stopień rozosiowania łączonych wałów, a więc komponent rozosiowania może nie być widoczny na widmie (ale jednocześnie takie rozosiowanie nie musi być szkodliwe). W przypadku wałów połączony tarczami, oprócz częstotliwości 2x, rozosiowaniu często towarzyszą kolejne harmoniczne parzyste, szczególnie komponent 4x [1]. Z kolei dla sprzęgieł zębatych, częstotliwość generowana na widmie jest często uzależniona od ilości zębów (tzw. kolców) sprzęgła. Niemniej jednak, warto pamiętać, że wiele maszyn przemysłowych zostało zmodernizowanych w trakcie eksploatacji (względem oryginalnej konstrukcji), co powoduje, że wpływ rozosiowania na dynamikę wirującego wału jest niższy niż spodziewany, co pokazano na przykładzie napędu wentylatora z sprzęgłem tarczowym, w którym zastosowano elastyczną tarczę [2]. W drugą stronę, nawet przy współosiowości wałów, dla układów obciążonych rozosiowanie może wystąpić z uwagi na różne rozłożenie sztywności, chociażby przez zastosowanie wpustów [3].

Kolejną trudnością w detekcji i identyfikacji rozosiowania jest niewspółosiowość wałów połączonych kołami zębatymi. Jak wskazano w Tabeli  2.1 w [3], może zdarzyć się, że wyosiowanie wałów redukuje komponent 2x tylko dla jednego wału, a dodatkowo wprowadza bardzo istotne zmiany w komponencie 1x dla obu wałów, co wskazuje, że w wielu konfiguracjach rozosiowanie i niewyrównoważenie są zjawiskami wzajemnie oddziałującymi – co naturalnie w praktyce utrudnia proces diagnostyczny.

Aby rozwiązać ten problem w ramach pomiaru drgań, dodatkowo analizuje się kierunek drgań, który również jest czynnikiem wpływającym na kształt widma maszyny rozosiowanej. Wg. norm (np. ISO 20816), rozosiowanie należy śledzić zarówno w osi pionowej (jak niewyrównoważenie), jak i w osi poziomej. Warto pokreślić, że z uwagi na opisane wcześniej czynniki (rodzaj rozosiowania, rodzaj i parametry pracy), wartości poszczególnych harmonicznych na widmie dla pomiaru w kierunku poziomym i pionowym mogą się różnić zasadniczo. Dlatego też, w ramach potrzeby, rozosiowanie identyfikuje się precyzyjnie za poprze detekcję zmiany fazy dla komponentu 2x w kierunku poziomym (chodzi o rozróżnienie rozosiowania od niewyrównoważenia, dla którego taka zmiana fazy typowo nie występuje). Alternatywnie, oprócz pomiaru drgań, problem rozosiowania rozwiązuje się często z wykorzystaniem przenośnych urządzeń laserowych.

Przykład laboratoryjny

Rysunek 4 przedstawia stanowisko AV TEST BENCH, które umożliwia wprowadzanie kontrolowanego stanu rozosiowania poprzez niewspółosiowe ustawienie dwóch części stanowiska, tj. w taki sposób, że wał szybki (Fast Shaft – FS) jest niewspółosiowy z Wałem Wolnym (Slow Shaft – SS) poprzez sprzęgło elastyczne. W trakcie pomiarów, prędkość obrotowa wału napędowego szybkiego wynosiła nominalnie 3000 RPM, a z uwagi na przełożenie (23/67), prędkość wału wolnego wynosiła 3000 RPM *23/67 = 1030 RPM. Pomiar był dokonywany na obudowie łożyska tocznego zaznaczonego na rys. 5

Rysunek 5 Wprowadzenie niewyrównoważenia na stanowisku AV TEST BENCH

Na rys. 6a przedstawiono fragment referencyjnego widma częstotliwościowego dla ustawienia współosiowego, a na rys. 6b przedstawiono analogiczny fragment widma częstotliwościowego dla ustawienia niewspółosiowego.

Kursor harmoniczny

Jak pokazano na Rys. 6 na przykładzie rozosiowania, w analizie diagnostycznej wykorzystuje się różnego rodzaju kursory, m.in.: kursor pojedynczy, kursor podwójny (informuje o odstępie w danej dziedzinie), kursor harmoniczny oraz kursor wstęg bocznych. W niniejszym poście wykorzystaliśmy kursor harmoniczny w środowisku VIBnavigator.

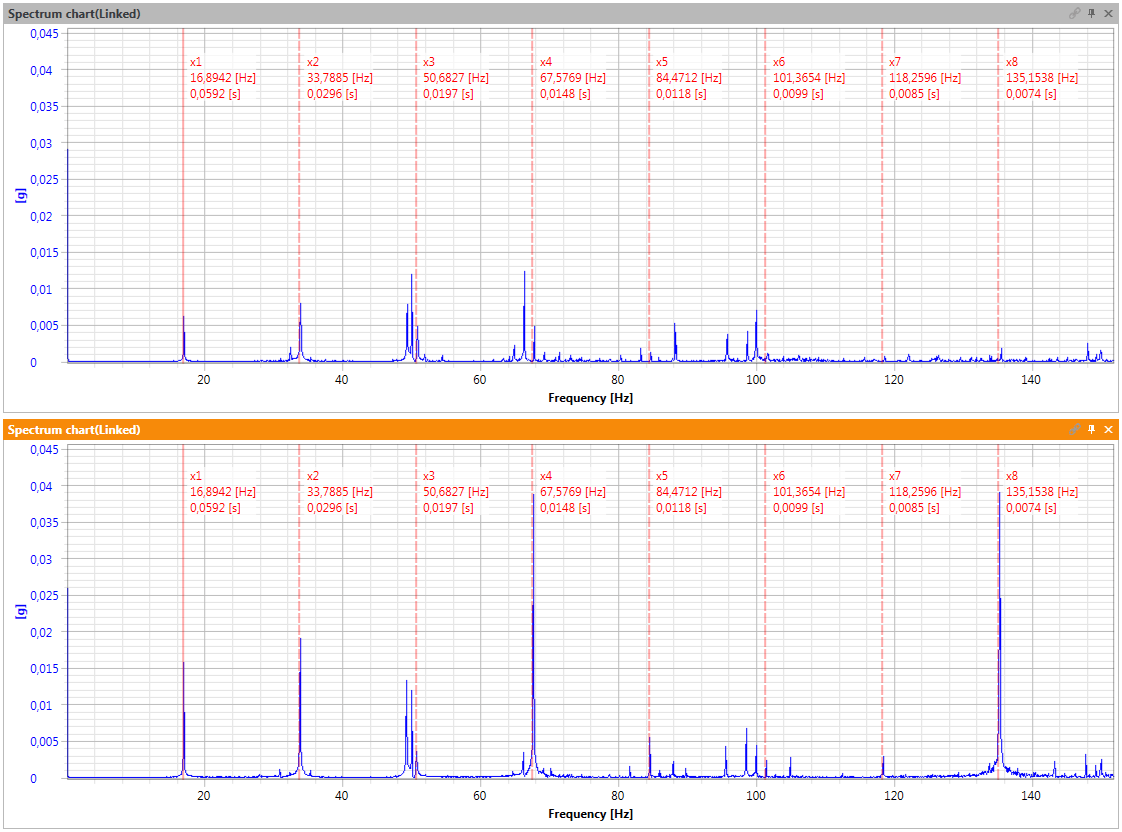
Rysunek 6 Widmo maszyny wirnikowej w stanie poprawnym (góra) oraz rozosiowanej (dół)

Rys. 6 wskazuje, że dla maszyny rozosiowanej, ma miejsce wzrost parzystych harmonicznych wału wolnego. Największy wzrost jest widoczny dla 8 oraz 4 harmonicznej, co jest spowodowane tym, że sprzęgło elastyczne ma 4 zęby (kły). Niedokładne pokrywanie się wartości dla kursorów wynika tylko z tego, że kursory zostały minimalnie przesunięte, aby nie zasłaniały komponentów. Pomiary były wykonywane praktycznie jeden po drugim i opisują maszynę różniącą się wyłącznie poziomem rozosiowania.

Zastosowanie aparatury pomiarowej

Firma AMC VIBRO oferuje zarówno detekcję, identyfikację i ocenę poziomu komponentu rozosiowania jako komponentu zdefiniowanego przez użytkownika, jak również jako komponentu charakterystycznego automatycznie wyliczonego przez system na podstawie modelu kinetostatycznego.

Tabela 2.1 Zestawienie urządzeń rodziny AVM pod kątem częstotliwości charakterystycznych

	AVM 1000	AVM 2000	AVM 4000
Detekcja rozosiowania analizą VRMS	✔️	✔️	✔️
Detekcja i identyfikacja analizą Shaft 2x w dziedzinie częstotliwości wyznaczoną ręcznie		✔️	✔️
Detekcja i identyfikacja analizą Shaft 2x w dziedzinie rzędów wyznaczoną ręcznie		✔️	✔️
Detekcja i identyfikacja analizą Shaft 2x w dziedzinie częstotliwości wyznaczoną automatycznie			✔️
Detekcja i identyfikacja analizą Shaft 2x w dziedzinie rzędów wyznaczoną automatycznie			✔️
Kursor pojedynczy		✔️	✔️
Kursor podwójny		✔️	✔️
Kursor harmoniczny		✔️	✔️
Kursor wstęg bocznych		✔️	✔️

Literatura

1. Dewell   L.,  Mitchell  L.  D., Detection of a misaligned disk coupling using spectrum analysis. Journal of Vibration, Acoustics, Stress, and Reliability in Design, 106, 1983
2. Zachwieja J., Analiza dynamiki wentylatora promieniowego w warunkach niewspółosiowości wałów wirnika i silnika, Diagnostyka 1 (53)/2010
3. B. Randall, Vibration-based condition monitoring, John Wiley & Sons, Ltd., 2011

Polecamy