A(M)Cademy of VIBROdiagnostics
#3 Co to jest częstotliwość charakterystyczna?
Zanim przejdziemy do wyjaśnienia zagadnienia „częstotliwości charakterystycznej” trzeba wyjaśnić delikatną różnicę pomiędzy kilkoma podobnymi pojęciami:
- komponent sygnału – składowa sygnału w dziedzinie czasu (głównie sinusoida albo szum),
- komponent widmowy – „prążek” widmowy albo coś innego na widmie, co jesteśmy w stanie zobaczyć, zmierzyć i opisać,
- komponent częstotliwościowy – „prążek” widmowy, którego częstotliwość możemy odczytać,
- komponent charakterystyczny – składowa sygnału, którą możemy odnieść do elementu maszyny,
- częstotliwość charakterystyczna – „prążek” widmowy, który możemy odnieść do elementu maszyny (zwyczajowo tą nazwę stosuje również – niewłaściwie – do dziedziny rzędów).
W optymistycznym scenariuszu diagnostyki maszyn, każdy element mechaniczny maszyny wirnikowej generuje unikatowy zestaw komponentów sygnału drgań. Rysunek 1 przedstawia symbolicznie przykładowe zestawy takich komponentów charakterystycznych, generowanych kolejno przez przekładnię zębatą, wał napędowy oraz łożysko toczne.
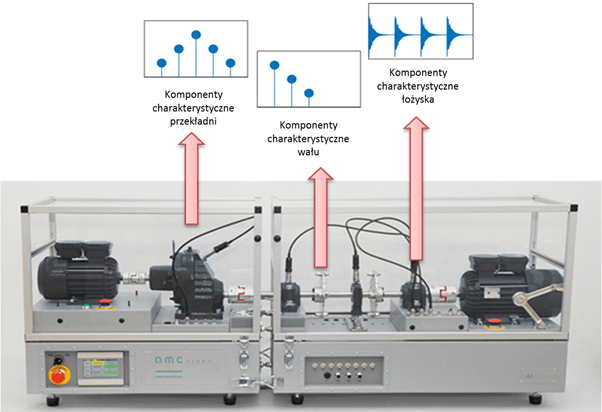
Rysunek 1 Komponenty charakterystyczne przekładni (dziedzina częstotliwości), wału (dziedzina częstotliwości) oraz łożyska (dziedzina czasu)
Na Rys. 1 przedstawiono dwa często występujące typy komponentów charakterystycznych w dziedzinie częstotliwości (czyli komponentów częstotliwościowych) – wstęgi boczne dla przekładni i komponenty harmoniczne dla wału oraz jeden typ komponentów charakterystycznych w dziedzinie czasu – odpowiedzi impulsowe dla łożyska.
W każdym przypadku, wszystkie komponenty sygnału są najpierw reprezentowane w oryginalnym sygnale drgań w dziedzinie czasu (rzadziej w dziedzinie kąta), ale potem ścieżki przetwarzania mogą być różne. Przykładowo, komponenty charakterystyczne łożyska na Rys. 1 pokazane w dziedzinie czasu są wynikiem obliczania obwiedni sygnału, która może być wykonana w dziedzinie częstotliwości. W konsekwencji, jeśli dany komponent widmowy jest analizowany na widmie obwiedni (a nie na widmie „zwykłym” oryginalnego sygnału), ten fakt powinien być zawsze odnotowany – gdyż taki sam komponent charakterystyczny na widmach różnego rodzaju może świadczyć o działaniu różnych sił na maszynę i sprowadza się do innego wniosku diagnostycznego.
Gdzie zatem zbiegają się pojęcia komponentu widmowego i częstotliwości charakterystycznej?
Znajomość „częstotliwości charakterystycznych” umożliwia częściowe przyporządkowanie komponentów widmowych do konkretnych elementów maszyny, łączy się więc z zagadnieniem identyfikacji uszkodzenia maszyny.
Chociaż nie jest to do końca oczywiste, komponenty charakterystyczne są pojęciem poprzedzającym pojęcie częstotliwości charakterystycznych i dodatkowo odnoszą się ogólnie do widma sygnału reprezentowanego w dziedzinie kąta, a więc do widma w dziedzinie rzędów, co będzie wyjaśnione krok-po-kroku. Innymi słowy, te dwa proste pojęcia są połączone jednym pojęciem nieco trudniejszym. Tabela 1 przedstawia zestaw przykładowych komponentów widmowych związanych z poszczególnymi elementami maszyny wirnikowej.
Tabela 1 Przykładowe częstotliwości charakterystyczne
| Element maszyny | Rodzaj wykresu | Komponent widmowy | Rodzaj uszkodzenia |
| Wał napędowy | widmo | 1x | niewyrównoważenie |
| Wał napędowy | widmo | 1x,2x | rozosiowanie |
| Wał napędowy | widmo | 1x, 2x, 3x | luzy posadowienia |
| Łopaty wentylatora | widmo | RPM*ilość_łopat | uszkodzona łopata |
| Przekładnia zębata | widmo | GMFx1,GMFx2 | uszkodzenie lokalne |
| Przekładnia zębata | widmo | DSBx1, DSBx2 | przekoszenie |
| Łożysko toczne | widmo obwiedni | BPFO 1x,2x,3x | lokalne uszkodzenie bieżni zewnętrznej |
Oznaczenia:
RPM – prędkość obrotowa,
GMF – częstotliwość zazębiania przekładni (ilość zębów na kole na danym wale * RPM),
DSB – wstęgi boczne (lewa i prawa),
BPFO – częstotliwość (uszkodzenia) bieżni zewnętrznej łożyska tocznego.
Należy pamiętać, że w praktyce wcale nie jest tak, że obecność danego komponentu świadczy o uszkodzeniu maszyny. Przykładowo, szereg harmonicznych wału jest typowy dla „zdrowych” kompresorów tłokowych. Wiele też zależy od konstrukcji – w przypadku przekładni z zębami prostymi najczęściej uszkodzenie manifestuje się wzrostem komponentów GMF, ale już dla przekładni o zębach skośnych, uszkodzenie manifestuje się wzrostem wstęg bocznych komponentów GMF. Można natomiast powiedzieć, że wykrywanie i obserwacja wzrostu energii częstotliwości charakterystycznych jest najpowszechniej stosowaną i najbardziej efektywną metodą wykrywania uszkodzeń maszyn wirnikowych.
Jak wcześniej wspomniano, w tabelach takich jak Tabela 1 podaje się charakterystyczne rzędy, a w ramach praktycznej analizy opisuje się charakterystyczne częstotliwości. Poniżej przedstawiamy opis tego przejścia wraz z przykładem.
Idea „charakterystycznych rzędów”
Rozważmy komponent częstotliwościowy ilustrujące niewyrównoważenie wału wolnego na stanowisku AV TEST BENCH, przedstawiony na Rys. 2
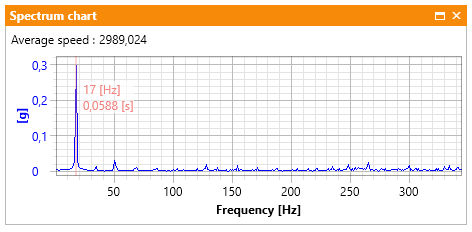
Rysunek 2 Niewyrównoważenie na widmie częstotliwościowym
Jeśli wał wolny maszyny obraca się z nominalną prędkością 1000 obr/min (1000 RPM), jego „częstotliwość charakterystyczna” wynosi:
f_char = 1000/60 = 16.7 Hz
co w przybliżeniu (dla rozdzielczości widmowej równej 1 Hz) daje 17 Hz. Na widmie w dziedzinie rzędów, „charakterystyczny rząd” tego wału jest związany z jego przełożeniem względem pomiaru prędkości obrotowej na wale szybkim. Na stanowisku AV TEST BENCH, przełożenie przekładni zębatej wynosi 23/67 = 0.343. Komponent charakterystyczny ilustrujący niewyrównoważenie wału wolnego na widmie w dziedzinie rzędów przedstawia Rys. 3. Dla przykładu, gdyby niewyrównoważony był główny wał szybki, na Rys. 3 obecny byłby inny komponent charakterystyczny w miejscu „Order = 1”.
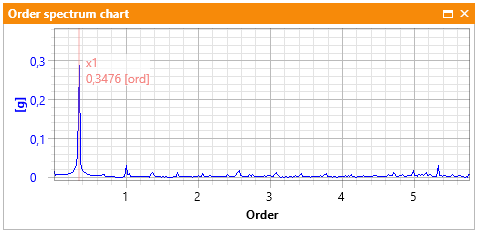
Rysunek 3 Niewyrównoważenie na widmie w dziedzinie rzędów
Poza wspomnianym zagadnieniem obliczeniowym, są jeszcze 2 istotne powody, dla których w praktyce diagnostycznej używa się widm w dziedzinie rzędów, o których wspomnimy:
1) Z uwagi na fluktuacje prędkości obrotowej w sygnałach rzeczywistych, komponenty częstotliwościowe są z reguły rozmyte. Warto zauważyć, że im wyższa częstotliwość komponentu deterministycznego (o pojedynczej częstotliwości), tym bardziej staje się on rozmyty. Z tego względu, w diagnostyce maszyn wirnikowych, zamiast analizy „częstotliwości charakterystycznych„, często analizuje się „charakterystyczne rzędy„. Przykładowo, Rys. 2 ilustruje typowe widmo częstotliwościowe dla stanu niewyrównoważenia wału napędowego. Dla porównania, Rys. 3 ilustruje ten sam stan na widmie w dziedzinie rzędów.
2) Poza mniejszym rozmyciem komponentów (szczególnie w wyższych częstotliwościach) najistotniejszą zaletą analizy w dziedzinie rzędów (względem analizy w dziedzinie częstotliwości) jest fakt, że wraz ze zmianą prędkości obrotowej, komponenty nie zmieniają swojego położenia na widmie.
Posiadając podstawową wiedzę o analizie rzędów, możemy teraz wrócić do kwestii częstotliwości charakterystycznych. Dla zainteresowanych – do tematu analizy w dziedzinie rzędów jeszcze wrócimy.
Przykład analizy
Jako przykład analizy częstotliwości charakterystycznych rozważmy komponenty charakterystyczne przekładni zębatej stanowiska AV TEST BENCH. Danymi, które znamy od producenta są:
- Z1 = 23: ilość zębów na kole małym (wał szybki – INPUT Shaft),
- Z2 = 67: ilość zębów na kole dużym (wał wolny – OUTPUT Shaft).
W pierwszym kroku, budujemy szablon kinetostatyczny w Edytorze Kinematyki w środowisku VIBnavigator. Gotowy schemat przedstawia Rys. 4.
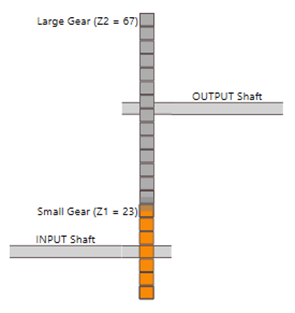
Rysunek 4 Schemat przekładni zębatej
Po zaznaczeniu wału referencyjnego (INPUT Shaft), Edytor Kinematyki w drugim kroku automatycznie oblicza charakterystyczne rzędy dla kilku kolejnych harmonicznych częstotliwości zazębiania GMF (z ang. Gear Meshing Frequency), a następnie, dla każdej z nich, oblicza charakterystyczne rzędy dla kilku kolejnych par podwójnych wstęg bocznych DSB (z ang. Double Side Bands). W Tabeli 2 przedstawiono wartości 4 GMF-ów oraz po dwie pary wstęg bocznych pochodzących od wału szybkiego i wału wolnego dla pierwszego GMF-a.
Tabela 1 Przykładowe rzędy charakterystyczne
| GMF harmonics | order |
| Przekładnia.GMFx1 | 23,00 |
| Przekładnia.GMFx2 | 46,00 |
| Przekładnia.GMFx3 | 69,00 |
| Przekładnia.GMFx4 | 92,00 |
| GMF sidebands | order |
| Przekładnia.GMFx1+Gear1x1 | 24,00 |
| Przekładnia.GMFx1+Gear1x2 | 25,00 |
| Przekładnia.GMFx1+Gear2x1 | 23,34 |
| Przekładnia.GMFx1+Gear2x2 | 23,69 |
| Przekładnia.GMFx1-Gear1x1 | 22,00 |
| Przekładnia.GMFx1-Gear1x2 | 21,00 |
| Przekładnia.GMFx1-Gear2x1 | 22,66 |
| Przekładnia.GMFx1-Gear2x2 | 22,31 |
W celu ilustracji, Rys. 5 przedstawia przykładowe widmo w dziedzinie rzędów, na którym zaznaczono częstotliwość charakterystyczną (ściślej: rząd charakterystyczny) zazębiania przekładni stanowiska AV TEST BENCH GMFx1 wraz z parą wstęg bocznych wału szybkiego (rząd 1, a więc 23+/-1) oraz dwiema prawymi i jedna lewą wstęgą boczną wału wolnego (rząd 0,343, a więc Prawa: 23+0,343*1, 23+0,343*2 i Lewa: 23-0,343*1).
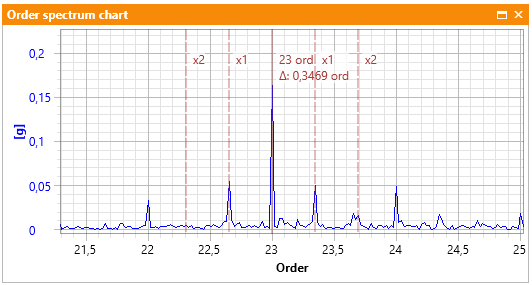
Rysunek 5 Komponent widmowy GMFx1i jego wstęgi boczne
Jak wspomniano wcześniej, w praktyce inżynierskiej, często odwołujemy się do nazw „częstotliwościowych” analizując dane w dziedzinie rzędów – sama nazwa komponentu GMF, z ang. „Gear Meshing Frequency” trochę nas do tego upoważnia.
Trzecim, bardzo ważnym inżynierskim krokiem jest (zawsze trochę subiektywne) jest zdefiniowanie matematycznej relacji pomiędzy „idealnym” rzędem charakterystycznym, a pasmem w dziedzinie rzędów. W praktyce, chodzi o to, aby każdemu zdefiniowanemu „prążkowi nadać jakąś szerokość” na widmie, którą będzie monitorował system diagnostyki. Tutaj często stosuje się wartość na poziomie 3%. Przykładowo, w ten sposób, „ładna” liczba 23 jest zamieniana na dwie „nieładne liczby”:
bin_start = 23 + 3%*23 = 23,69 (rząd)
bin_stop =23 – 3%*23 = 22,31 (rząd)
Najczęściej jednak, ta operacja jest niewidoczna dla użytkownika systemu monitorowania.
W ostatnim kroku, charakterystyczne rzędy bin_start i bin_stop są zamieniane na finalne częstotliwości charakterystyczne wg. przepisu:
f_char_start = bin_start * średnia prędkość maszyny [Hz]
f_char_stop = bin_stop * średnia prędkość maszyny [Hz]
Oczywiście, w ramach przygotowań do analizy diagnostycznej, często przekształca się „idealne” charakterystyczne rzędy w „idealne” charakterystyczne częstotliwości, wykorzystując średnią prędkość maszyny, np.: prędkość_średnia = 1000 HzGMF = 23 (rząd)f_char_GMF = 23 * 1000/60 Hz = 383,3 Hz
W ten sposób wiemy, że komponent w bliskiej okolicy 383 Hz jest prawdopodobnie związany z zazębianiem tej przekładni.
Co nam dają komponenty charakterystyczne?
Bardzo wiele! W praktyce diagnostycznej, komponenty charakterystyczne są używane na dwa główne sposoby. Jeśli mówimy o dużym systemie monitorowania, definicja charakterystycznych rzędów/częstotliwości jest podstawą konfiguracji systemu w zakresie analiz wąskopasmowych. Dobrze zdefiniowane analizy wąskopasmowe opisane nazwą elementu mechanicznego stanowią klucz do skutecznego monitorowania stanu technicznego obiektu, co pokazano ideowo na Rys. 6.
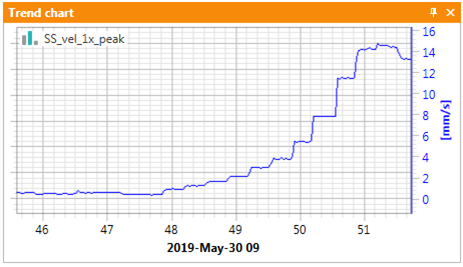
Rysunek 6 Gwałtowny rozwój niewyrównoważenia wirnika pomy
Jeśli mówimy o analizie danych (diagnostyka techniczna), charakterystyczne rzędy/częstotliwości pomagają nam identyfikować komponenty widmowe – od czego tak naprawdę zaczęliśmy bieżący post! Przykład identyfikacji znajdziemy na Rys. 5.
Zastosowanie aparatury pomiarowej
Firma AMC VIBRO oferuje zarówno pomiar komponentów charakterystycznych zdefiniowanych przez użytkownika, jak również komponentów charakterystycznych automatycznie wyliczonych przez system na podstawie modelu kinetostatycznego.
Tabela 2 Zestawienie urządzeń rodziny AVM pod kątem częstotliwości charakterystycznych
| AVM 1000 | AVM 2000 | AVM 4000 | |
| Śledzenie charakterystycznych komponentów użytkownika w dziedzinie częstotliwości | ✔️ | ✔️ | |
| Śledzenie charakterystycznych komponentów użytkownika w dziedzinie rzędów | ✔️ | ✔️ | |
| Automatyczne wyznaczanie rzędów charakterystycznych elementów maszyn | ✔️ | ||
| Automatyczne wyznaczanie częstotliwości charakterystycznych elementów maszyn | ✔️ |