A(M)Cademy of VIBROdiagnostics

18.02.2021

Drgania to okresowe przemieszczenie obiektu mechanicznego w czasie. Obok wzrostu temperatury i tarcia, są jedną z form rozpraszania energii dostarczonej do obiektu takiego jak samochód, samolot, wentylator, pompa, czy pralka. Z tego powodu, drgania mogą powiedzieć bardzo dużo o stanie technicznym urządzenia.

W systemach pomiarowych, drgania mogą być mierzone jako jedna z trzech różnych wielkości fizycznych: jako sygnał przemieszczenia, prędkości i przyspieszenia. Przemieszczenie jest głównie używane w monitorowaniu stanu technicznego względnie dużych wałów osadzonych w łożyskach ślizgowych (tworzy się z nich m.in. tzw. wykresy orbit dla turbozespołów). Prędkość drgań jest podstawową miarą zgodnie z normami drgań (takimi jak ISO 20816), ponieważ najdokładniej odzwierciedla niebezpieczne siły działające na maszynę w najszerszym zakresie częstotliwościowym. Wybór właściwej wielkości pomiarowej jest bardzo ważny, wpływa na jakość otrzymanego pomiaru i – oczywiście – na cenę. Przyspieszenie drgań jest obecnie techniką pomiaru drgań #1 na świecie, ponieważ czujniki przyspieszenia są najtańsze i najłatwiejsze w użyciu, umożliwiają analizę drgań strukturalnych, a także pozwalają obliczyć prędkość i przemieszczenie drgań. Jak się więc mają do siebie te 3 wielkości?

Trochę teorii

Rys. 1 przedstawia przykładowy, sinusoidalny sygnał przyspieszenia (Acc) o częstotliwości 100 Hz i amplitudzie 7 [g], skonwertowany kolejno na sygnał prędkości (Vel) i przemieszczenia (Dis). Zauważ jak zmieniają się jednostki sygnałów z [g] kolejno na [mm/s] i [mm]. W pokazanym przykładzie, amplituda sygnału prędkości wynosi 109.3 [mm/s], ponieważ obliczenie amplitudy sygnału prędkości wymaga zarówno konwersji jednostek (1 [g] = 9.81 [m/s2] = 9810 [mm/s2]), jak i przeskalowania amplitudy przez wartość 1/1/(2∙π∙f), gdzie w naszym przypadku f = 100 [Hz]. Amplituda sygnału przemieszczenia obliczana jest mnożąc ponownie wartość amplitudy sygnału prędkości przez współczynnik 1/1/(2∙π∙100). Jak widać na rys. 1, konwersja wartości fizycznych nie zmienia wartości częstotliwości komponentów. W taki właśnie sposób można przeliczać między sobą wielkości opisujące drgania. Warto dodać, że z reguły sygnał przyspieszenia będzie najbardziej zaszumiony, a przemieszczenia – najmniej.

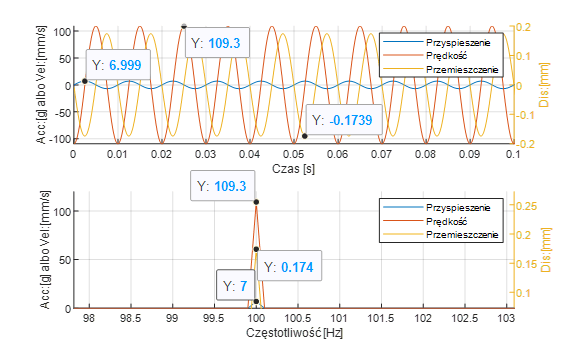
Rysunek 1 Przyspieszenie, prędkość i przemieszczenie komponentu sinusoidalnego.

W przypadku analizy widmowej, wybór wartości fizycznej przekłada się na zmianę kształtu widma. Jak pokazano symbolicznie na rys. 2, sygnał przyspieszenia wzmacnia komponenty wysokoczęstotliwościowe, a sygnał przemieszczenia wzmacnia komponenty niskoczęstotliwościowe.

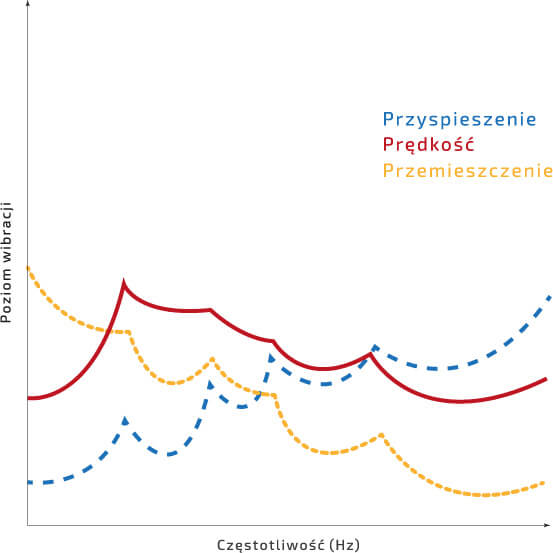
Rysunek 2 Schemat porównawczy widma sygnału przyspieszenia, prędkości i przemieszczenia

Analiza praktyczna

Jakie to ma znaczenie w praktyce? Wartości amplitud drgań będą się zmieniały w zależności od wybranej wielkości fizycznej. Jeżeli sygnał drgań będzie miał stałą prędkość, wraz ze wzrostem częstotliwości, zwiększać się będzie wartość przyspieszenia, a maleje wartość przemieszczenia drgań. Analogicznie, wraz ze spadkiem częstotliwości, wzrasta wartość przemieszczenia, a maleje wartość przyspieszenia, co pokazano schematycznie na rys. 3. Przedstawia on zmianę wielkości fizycznych drgań dla sygnału drgań o częstotliwości 5 Hz oraz 500 Hz.

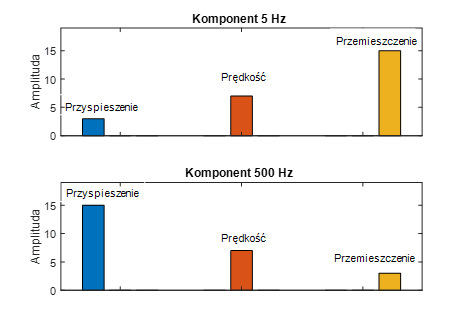
Rysunek 3 Schematyczne zmiany wartości komponentów

Analiza różnych wielkości fizycznych jest korzystna w sytuacjach, kiedy monitorujemy jednocześnie liczne komponenty generowane w szerokim paśmie częstotliwościowym. Rys. 4 przedstawia maszynę wirnikową złożoną (od lewej) z silnika napędowego, przekładni równoległej, wałów, zespołu łożysk oraz silnika hamującego. Na rys. 4 przedstawiono schematycznie ogólny rodzaj komponentów generowanych przez wał napędowy, przekładnie i łożysko oraz zaznaczono typowe zakresy częstotliwościowe, w których manifestują się uszkodzenia tych elementów. Ponieważ wały napędowe typowych maszyn obracają się nie szybciej niż 50-60 Hz, często monitorowana jest prędkość ich drgań lub przemieszczenie (szczególnie dla łożysk ślizgowych). W przypadku przekładni zębatych, do około 160 Hz (dotyczy wszystkich istotnych harmonicznych) zalecany jest pomiar prędkości drgań, a powyżej 500 Hz z reguły stosowany jest pomiar przyspieszenia. W przypadku wzbudzania drgań strukturalnych, typowych dla uszkodzeń łożysk tocznych oraz niektórych uszkodzeń przekładni zębatych, konieczny jest pomiar przyspieszenia, gdyż maszyny wirnikowe najczęściej wykazują drgania strukturalne w zakresie od 2 kHz do 20 kHz.

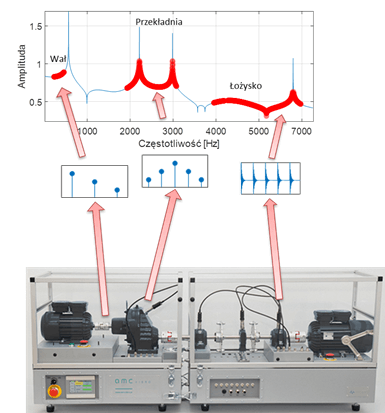
Rysunek 4 Pasma częstotliwości wzbudzane przez elementy maszyny wirnikowej

Zastosowanie aparatury pomiarowej

Firma AMC VIBRO oferuje diagnostykę maszyn przemysłowych z wykorzystaniem nowoczesnych urządzeń serii AVM 1000, AVM 2000 oraz AVM 4000. Seria AVM1000 to 1-kanałowe proste w obsłudze systemy umożliwiające pomiar wartości szczytowej 0-PEAK i wartości skutecznej drgań RMS sygnału przyspieszenia lub sygnału prędkości. Seria AVM 2000 oferuje funkcjonalność AVM1000 oraz dodatkowo umożliwia analizę sygnału obwiedni z sygnału przyspieszenia oraz wyznaczenie mocy w wyznaczonych pasmach częstotliwościowych zarówno dla sygnału przyspieszenia, jak i prędkości. System AVM4000 umożliwia pomiar dowolnej wielkości fizycznej w standardzie EPE (ICP) oraz wyznaczenie analiz użytkownika z dowolnie wybranej wielkości fizycznej sygnału, tj. zarówno przyspieszenia drgań, prędkości, jak również przemieszczenia. Główne cechy urządzeń pod kątem przetwarzanych wartości fizycznych przedstawiono w tabeli 1. Wszystkie te wartości są wyliczane wewnątrz modułów z sygnału przyspieszenia drgań.

Tabela 1 Zestawienie urządzeń rodziny AVM pod kątem przetwarzanych wartości fizycznych

	AVM 1000	AVM 2000	AVM 4000
0-Peak przyspieszenia	✔️	✔️	✔️
0-Peak prędkości	✔️	✔️	✔️
RMS przyspieszenia	✔️	✔️	✔️
RMS prędkości	✔️	✔️	✔️
Obwiednia przyspieszenia		✔️	✔️
Moc w pasmach przyspieszenia		✔️	✔️
Szerokopasmowe estymaty użytkownika sygnału przyspieszenia			✔️
Szerokopasmowe estymaty użytkownika sygnału prędkości			✔️
Szerokopasmowe estymaty użytkownika sygnału przemieszczenia			✔️
Wąskopasmowe estymaty użytkownika sygnału przyspieszenia			✔️
Wąskopasmowe estymaty użytkownika sygnału prędkości			✔️
Wąskopasmowe estymaty użytkownika sygnału przemieszczenia			✔️

Polecamy